前言
数据校验是计算机发展至今的至关重要的部分。但是它一般作为底层、后台或者内置模块出现,因而即使对于多数成天在计算机网络里飘荡的人来也说并不十分了解。前段时间由于特殊原因深入学习了一下MD5,后面接着学习了SHA-1和CRC32。
当前最常用的三个数据校验算法CRC、MD5和SHA-1当中,强度(这个强度是相对于被破解的困难程度来说的)以CRC最弱,而SHA-1最强。其实三个算法的原理和实现都很简单(CRC优化的算法可能比较费解),下面依次讲起,并对各算法的当前破解情况进行了介绍,在相应之处列有比较详细的参考文档。
CRC是什么?CRC的全称是Cyclic Redundancy Checksum,即“循环冗余校验码”。简单的说它是一种利用二进制的多项式除法来取得数据的校验和的方法。
CRC有什么用?目前主要使用在哪些地方?一如其名,CRC对数据的处理结果是取得一个校验码,在数据传输的前后分别计算一次,然后进行比较就可以发现是否有错误发生。打一个不是很恰当的比方,你乘车前检查了一下钱包,里面有N张RMB,下车的时候你再检查一次,如果不是N张RMB的话你就会应该意识到出问题了(不过这种情况下一般是会减少吧),但如果还是N张RMB的时候是否能保证没有出问题了呢——很不幸,不一定,有可能被人家换了几张小额的给你,或者换了假币给你,这就类似于后边要讲到的“CRC碰撞”。CRC广泛应用于以太网的数据包检查,PNG,以及我们常用的压缩软件(PKZIP, Zlib,WinRAR……)等。
CRC原理是什么?原理其实非常简单,就是二进制的多项式除法。
目的(为什么需要CRC)
数据在传输时一般希望具有以下特性的一种或多种:
- 机密性,信息的内容不想被别人偷看;例如A给B写了一封信,担心信被别人拿到然后偷看了其中的内容,A可能会用某种加密方式(这种方式是和B约定好的)给信的内容加密,只有B能阅读信的内容。
- 完整性,信息不希望发生丢失;还是上面的例子,A给B写了一封信,担心信在邮寄过程中损坏,A可能会在信上做一些特殊的标记(这种方式是和B约定好的),然后B拿到信之后,通过检查标记就能知道信的内容是否完整。
- 收发方鉴别,能够确认信息是谁发过来的;还是上面的例子,A给B写了一封信,B能够通过信上的特定信息确定这封信是A写的。
CRC就是用于保证数据的完整性。
为了保证数据的“完整性”,前辈们发明的一种方法就是在要发送的数据后面加一个数,这个数是基于要发送的数据计算出来的值,通常称为校验和(checksum,这个词开始可能是描述通过sum方式计算出来的校验值,经过发展,现在是用于描述这个添加的校验值的通用术语),本文要讨论的CRC就是计算checksum的一种方法。在介绍CRC之前,我们先选一种简单的方法来计算checksum:将数据以字节为单位加起来,然后除以256,把余数作为checksum。
注意checksum这种方式的本质:把原始数据的部分信息提取到checksum中,进而使得不同数据的checksum会有所区别
所有数据均为16进制 原始数据 :1F C0 03 22 原始数据+校验和 :1F C0 03 22 04 接收方收到的数据 :1F C0 83 22 04
从上面的数据我们可以观察:1) checksum是如何计算的,2) 接收方如何利用checksum判断报文发生了变动;
发送报文的校验和是0x4(0x1F+0xC0+0x03+0x22=0x104,转换为10进制是260,除以256的余数就是4),数据在发送过程中可能受到了外部干扰,导致数据变动,接收方收到数据之后,重新计算校验和,发现应该是0x84(0x1F+0xC0+0x83+0x22=0x184,除以256的余数就是0x84),这样接收方就知道数据在传送过程中发生了变动,然后接收方可以决定是否要丢弃掉这条消息。
这种方法看起来还不错,为什么还需要别的方法呢?
因为采取这种方式时,不同数据的校验和容易重复,例如下面的一系列数据的校验和都是04,可以观察到这种校验方式无法区分数字相同,位置不同的情况。
原始数据+校验和 :04 00 00 00 04 原始数据+校验和 :00 00 04 00 04 原始数据+校验和 :02 00 02 00 04 原始数据+校验和 :00 01 00 03 04
再看看另外一个极端,既然checksum本质上是要提取原始数据的信息,然后还需要不同数据的checksum不会重复,那么直接把原始数据复制一份放在后面不就是完整保留了原始数据的信息吗?
原始数据+校验和 :01 FF 2C 00 01 FF 2C 00
相信大家很快看出来这种方式有什么问题,就是传输数据的效率太低,一条8个字节的报文中只有4个字节是有用的,剩余的只是用来保证数据的完整性。(磁盘数据备份中的RAID1就是用的这种完全备份的方式;看来不同的应用领域都有一些重要思想的应用,不同的设计也都有其应用场景。)
在简单的计算方案和完全备份的方案之间,出现了很多中间方案,CRC,哈希(Hash)就是其中的两种,只不过CRC在汽车行业报文传输中用得比较多,哈希则在文件传输上用得比较多(下载文件的时候,有时会看到下载的地方提供了一个哈希值,就是让你检查下载完的文件是否也有相同的哈希值,哈希方法在很多地方都有应用,并不局限于此)。
保证数据完整性方法的评价维度
在这里有必要思考一下评价维度的问题,解决任何一个问题都可能有很多方法,那么就必须有一些维度来评价这些方法,甚至指导探索新的方法,我认为在评价保证数据完整性的方法中可能有以下几个维度:
- 不同数据出现重复checksum的概率,越低越好
- 计算checksum的需要资源和时间,越少越好
- checksum占的空间,越少越好
维度2和3都需要以发展的眼光来看待,随着技术的发展,也许现在计算或者存储困难的问题,以后都能够轻而易举的解决。
计算方法
模2运算
因为CRC的计算涉及到模2运算,所以先说一下模2运算,模2运算是一种二进制运算的方法,与四则运算类似,不同的是模2运算不考虑进位和借位。
大家可能有疑惑,为什么CRC计算中会用模2运算,而不能用正常的四则运算?
这个我不清楚,我尽量不去纠结了。感兴趣的可以深挖一下~~
其中一点可以注意:因为运算中不进位,也不借位,所以每一位的运算结果不会影响其他位。
下面是模2加法,模2减法和异或的运算规则,可以发现模2加法,模2减法和异或有同样的结果。
模2加法 0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 0 (无进位) 模2减法 0 - 0 = 0 0 - 1 = 1 (无借位) 1 - 0 = 1 1 - 1 = 0 异或 0 xor 0 = 0 0 xor 1 = 1 1 xor 0 = 1 1 xor 1 = 0
下面看模2除法,初看的时候可能会比较疑惑,总体上与正常的除法是类似的,只不过在模2运算中数与数的大小关系与通常的理解不一致。
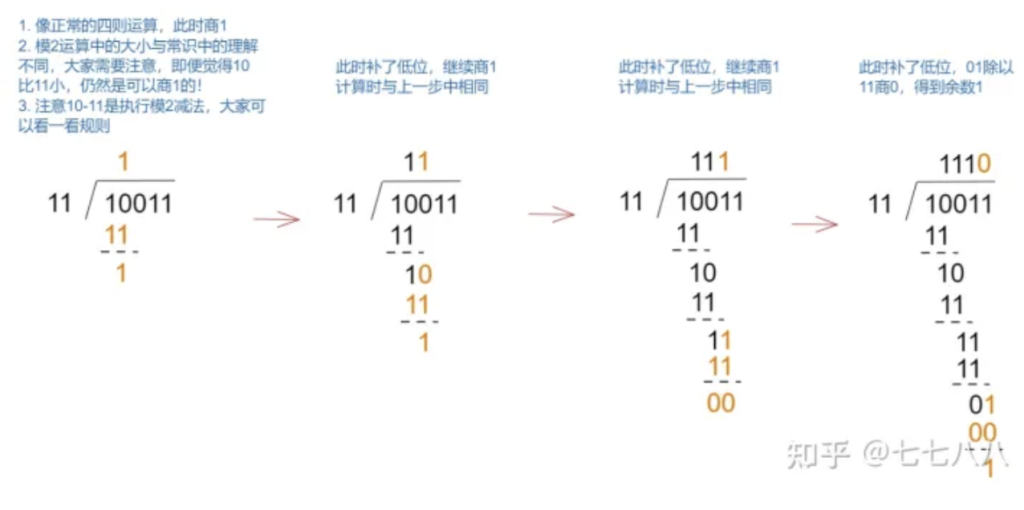
CRC计算
接下来看计算CRC的例子
原始数据是:1101011011
多项式:

把上面多项式中各项的系数取出来依次排列构成除数:10011(至于为什么不直接用这个数字,而是有一个多项式,我不清楚)
把原始数据后面加4(上面多项式最高幂次为x^4)个0构成被除数:1101011011–0000(原始数据–填充位)
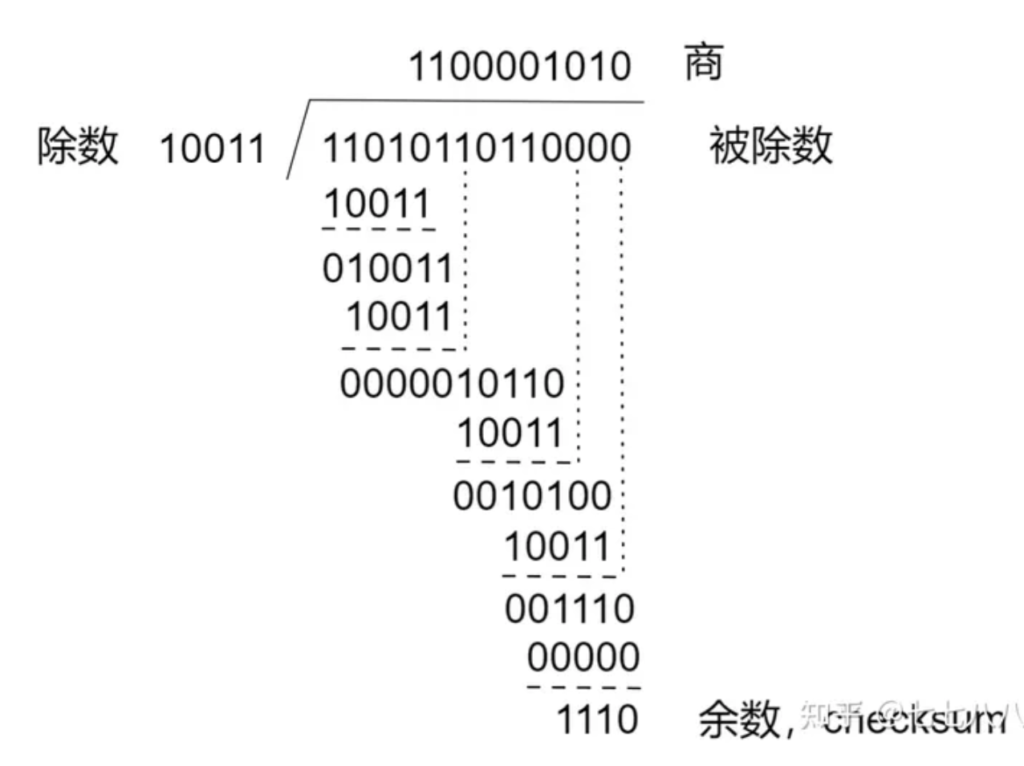
如下图所示为这个除法的计算过程(模2除法)
算出来的余数为1110,这就是checksum,增加了checksum的数据就是:
1101011011–1110(原始数据–checksum)
常用的CRC计算方法
有了上面的计算体验,大家可能对CRC已经有了一些感觉,实际工作中会有不同的CRC计算方式,这些方式的通常都是经过验证的效果比较好(应该是checksum重复概率比较低)的,因此通常会去直接使用这些计算方式。
根据checksum的长度(单位是bit)不同,常用的有:
CRC8,CRC16,CRC32的checksum长度分别占8位,16位,32位
根据使用的多项式或其他一些信息不同也会区分,例如:
CRC16_CCIT_ZERO:使用的多项式是0x1021(指CRC校验的多项式的二进制码去掉最高位)
CRC16_ARC:使用的多项式是0x8005